und der Mittelpunktswinkel einer Seite



Um regelmäßige Vielecke zu zeichnen, brauchst du Hilfe aus der Mathematik. Im Kern geht es um Folgendes:
 |
 |
und der Mittelpunktswinkel einer Seite |
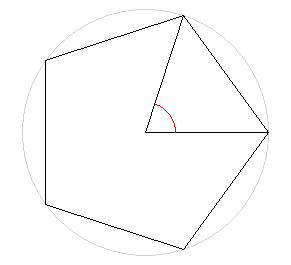
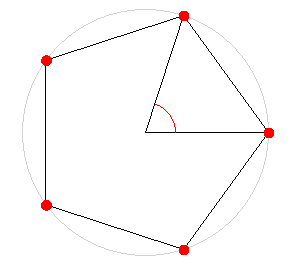
Die Eckpunkte eines regelmäßigen Vielecks liegen auf einem Kreis, dem sogenannten Umkreis des Vielecks.
Der Mittelpunktswinkel einer Seite eines regelmäßigen Vielecks beträgt
360°/n
wo n die Anzahl der Ecken des Vielecks ist. Im regelmäßigen Fünfeck beträgt dieser Winkel 72°. (In der Zeichnung rot markiert)
Um ein regelmäßiges Vieleck zu zeichnen, benötigst du eine Formel, die dir die Koordinaten seiner Eckpunkte auf dem Umkreis liefert. Eine solche Formel gibt es, sie ist sogar einfach und sie ist - was durchaus wichtig ist - auch einfach zu programmieren.
Einen Schönheitsfehler haben die nachfolgenden Formeln allerdings: Sie verwenden die trigonometrischen Funktionen Sinus und Cosinus, die je nach Schulart erst in der 9. oder in der 10. Klasse durchgenommen werden. Jüngeren Schülern bleibt also nur, die folgenden Formeln zu übergehen und die anschließend angegebenen Programmteile einfach zu verwenden.
Es gilt die folgende Regel:
Für einen Kreis mit Mittelpunkt (0, 0) und Radius 1 ergeben sich die Koordinaten der Punkte des Kreisbogens aus den Formeln:
x-Koordinate: x = cos(φ) y-Koordinate: y = sin(φ)
wo der Winkel φ der von der positiven x-Achse gemessene Mittelpunktswinkel zum Punkt (x. y) ist. Um alle Punkte des Kreisbogens zu erhalten, muss φ die Werte von 0° bis 360° durchlaufen.
Für einen Kreis mit beliebigem Mittelpunkt und Radius lautet die Verallgemeinerung dieser Regel:
Für einen Kreis mit Mittelpunkt M(xM, yM) und Radius r ergeben sich die Koordinaten der Punkte des Kreisbogens aus den Formeln:
x-Koordinate: x = r * cos(φ) + xM y-Koordinate: y = r * sin(φ) + yM
Diese Formeln kannst du ohne weiteres auch dann anwenden, wenn du die Funktionen Sinus (sin) und Cosinus (cos) noch nicht in der Schule durchgenommen hast. Es genügt völlig, zu wissen, dass diese beiden Funktionen dir für einen gegebenen Winkel die Koordinaten eines Punktes auf dem Kreisbogen liefern. Genaugenommen musst du das nicht einmal wissen, es genügt, dass du das Programmstück übernimmst, das ich dir gleich zeigen werde.
In C# heißen die benötigten Funktionen Math.Sin() und Math.Cos().
Für die praktische Verwendung beider Funktionen ist noch eine technische Besonderheit zu beachten:
Die Funktionen Math.Sin(), Math.Cos() erwarten ihr Funktionsargument nicht in Winkelgraden, sondern in einer anderen Darstellung, die in der praktischen Mathematik als das Bogenmaß bekannt ist.
Aus dem Winkelmaß φ berechnest du das Bogenmaß mit dieser Formel:
bogen = φ * π / 180°
wo π die bekannte Kreiszahl 3,1415926... ist.
Die folgende Zeichnung veranschaulicht den Zusammenhang von Winkelmaß und Bogenmaß:
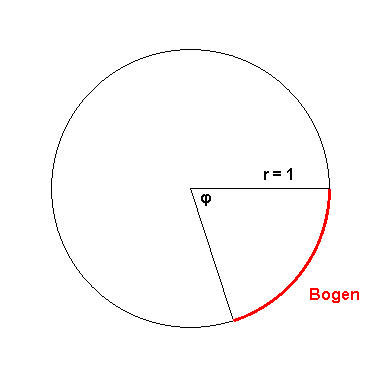
Wenn der Winkel φ zunimmt, vergrößert sich auch die Länge des dem Winkel zugeordneten Bogens im Einheitskreis. Wenn du dir das vorstellst, solltest du verstehen, dass man die Größe eines Winkels ebenso gut durch die Länge eines Kreisbogenabschnitts auf dem Einheitskreis wie durch ein Winkelmaß angeben kann.