Graphics: Rechtecke zeichnen

Dass Graphics eine Rechtecksfläche farbig füllen kann, haben wir schon gesehen. Trotzdem gucken wir uns jetzt ein etwas raffinierteres Beispiel genau an.

Kopiere also die folgenden Anweisungen in den Anweisungsteil der Methode InhaltZeichnen() und führe das Programm anschließend aus:

using (SolidBrush pinsel = new SolidBrush(Color.White))
{
     g.FillRectangle(pinsel, rechteck);  //Hintergrund zeichnen

       //rotes Rechteck zeichnen
     pinsel.Color = Color.FromArgb(128, 0, 0);
     g.FillRectangle(pinsel, 
                     new Rectangle (rechteck.Location,
                                    new Size(120, 120)));

       //grünes Rechteck zeichnen
     pinsel.Color = Color.FromArgb(0, 128, 0);
     g.FillRectangle(pinsel,
                     new Rectangle(rechteck.Location + new Size(50, 50),
                                   new Size(120, 120)));

       //blaues Rechteck zeichnen
     pinsel.Color = Color.FromArgb(0, 0, 128);
     g.FillRectangle(pinsel,
                     new Rectangle(rechteck.Location + new Size(100, 100),
                                   new Size(120, 120)));
}

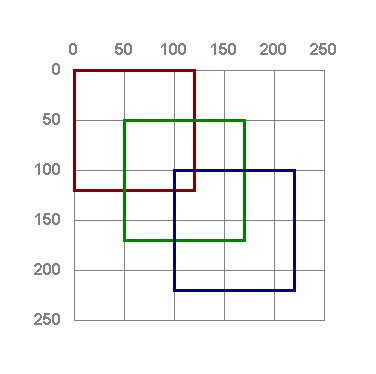
Dieses Programmstück erzeugt das folgende Bild:

Hier füllen wir zunächst das ganze Fenster mit einem weißen Hintergrund. Anschließend zeichnen wir ein dunkelrotes, ein dunkelgrünes und ein dunkelblaues Rechteck. Diese Rechtecke sind gleich groß aber sie sind unterschiedlich positioniert, so dass sie einander teilweise überdecken. Aus der Überdeckung erkennst du, in welcher Reihenfolge die Recktecke gemalt wurden.

In diesem Programmstück erzeugst du mehrfach neue Objekte. Das machst du mit Ausdrücken wie

new SolidBrush(Color.White)

oder

new Size(120, 120)

Das Schlüsselwort new zeigt hier an, dass nun ein Objekt neu erzeugt (instantiiert) wird. Dem Schlüsselwort folgt eine besondere Methode, die Konstruktor genannt wird. Ein Konstruktor wird oft mit Argumentwerten aufgerufen, die im neu zu erzeugenden Objekt gespeichert werden. Dieses Verfahren liefert ein sofort gebrauchsfähiges Objekt.

Wenn du nachzählst, findest du heraus, dass du in dem oben angegebenen Programmstück neun Konstruktoren hast.

Das Koordinatensystem einer Zeichenfläche

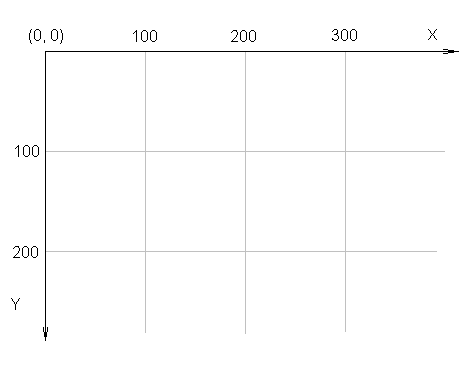
Um die Position eines Punktes auf der Zeichenfläche angeben zu können, verwenden wir ein Koordinatensystem, in dem jeder Punkt durch Angabe eines Wertes auf der x-Achse und eines Wertes auf der y-Achse eindeutig bestimmt ist.

Die Werte entlang der x-Achse nehmen von links nach rechts zu, die Werte entlang der y-Achse nehmen von oben nach unten zu. Beachte, dass der Wertverlauf entlang der y-Achse nicht der im Mathematikunterricht üblichen Verlaufsrichtung von unten nach oben entspricht, sondern gerade umgekehrt ist.

Das Bild zeigt das Koordinatensystem einer Zeichenfläche:

Da die Werte entlang der y-Achse von oben nach unten zunehmen, wirst du, wenn du Diagramme in der gebräuchlichen Form zeichen willst, gelegentlich umrechnen müssen. Darauf werde ich noch zu sprechen kommen.

Hier habe ich die Umrisse der drei Rechtecke in ein Koordinatensystem gezeichnet, aus dem du die Koordinaten der linken oberen Ecken aller drei Rechtecke mühelos ablesen kannst.